Можно ли быстро научиться умножать в уме, не прибегая к помощи калькулятора? Да, этому можно научиться, даже если ваш ребенок не вундеркинд. В этой статье поделимся несколькими работающими методами, которые помогут развить навык быстрого умножения чисел.
Раскладка по разрядам
Это самый простой прием для быстрого умножения двузначных чисел. Каждый из множителей необходимо разбить на десятки и единицы, а потом перемножить друг на друга эти новые числа, а результаты сложить. Этот способ подойдет тем, кто умеет удерживать в памяти одновременно до 4 чисел, хорошо знаком с таблицей умножения, умеет складывать в уме двузначные и трехзначные числа, не забывая по пути промежуточные результаты. Прокачать необходимые навыки можно путем тренировок зрительной памяти и визуализации, а также потренировав навык умножения на тренажере. Когда начнете овладевать этим методом, на первых порах можно фиксировать промежуточные результаты на бумаге, а затем, в ходе постоянных тренировок, постепенно переводить все действия в устный формат.
Например, нам нужно узнать, сколько будет 23х14.
Производим следующие действия:
23х14 = (20+3)х(10+4) = 20х10 + 3х10 + 20х4 + 3х4 = 200 + 30 + 80 +12 = 322
А еще можно произвести это умножение в 3 действия:
- Перемножить между собой десятки
- Перемножить каждую из единиц на десятки и прибавить к первому результату
- Умножить единицы на единицы и прибавить ко второму результату
Выглядеть это будет так:
23х14 = (20+3)х(10+4) = 20х10 + (3х10 + 20х4) + 3*4 = 200 + 110 +12 = 322
Подгонка чисел
Для этого способа достаточно привести к удобному виду заданное арифметическое вычисление.
Например, 12Х49 = (12х100)/2 – 12 =588.
В некоторых случаях этот способ может упростить и ускорить расчеты, однако он не является универсальным.
Визуализация умножения в столбик
А вот этот способ – самый универсальный для быстрого умножения чисел в уме. Заодно он развивает память и пространственное воображение. Метод подойдет для тех, кто освоил умножение в столбик. Для того, чтобы овладеть этой техникой устного умножения, следует вначале потренироваться в умножении двузначных чисел на однозначные в уме. А еще прокачать навык умножения можно в тренажере.
Освоив это, вы легко сможете устно умножать числа в три действия:
- Умножаем двузначное число на десятки второго числа.
- Умножаем двузначное число на единицы второго числа.
- Складываем полученные результаты.
Например: 23х15 = (23х10) + (23х5) = 230 + 115 = 345
Китайское умножение (иногда его называют японским умножением)
В азиатских школах детей учат умножению не в столбик, а с помощью рисования линий. Метод очень красивый, и сложный только на первый взгляд. На самом деле, его легко освоить и он очень наглядный и эффективный.
Для того, чтобы узнать, сколько будет 12х14 китайским методом, нужно нарисовать на листе линии, соответствующие количеству десятков и единиц. Десятки рисуем в правой части, а единицы – в левой. Сначала число 12: оно будет выглядеть, как одна линия справа и две слева.
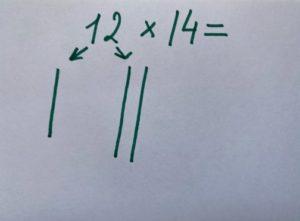
Таким же образом приступим к рисованию числа 14, но так, чтобы линии второго числа пересекались с линиями первого, то есть перпендикулярно линиям первого числа. 14 на бумаге будет выглядеть так: одна палочка сверху и 4 снизу.
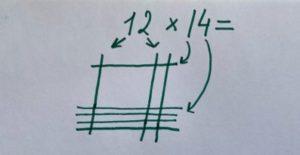
Как видите, у нас появились пересечения. Их нужно разделить на сотни, десятки и единицы следующим образом. Все пересечения в левом верхнем углу – сотни, в правом верхнем и левом нижнем углах – десятки, а в правом нижнем углу – единицы.
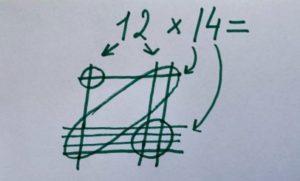
Начинаем считать:
- в сотнях у нас одно пересечение, значит, первая цифра ответа – 1
- в десятках – 6 пересечений, значит, вторая цифра в ответе – 6
- в единицах мы видим 8 пересечений, значит, третья цифра – 8.
Мы получили ответ на задачу: 12х14 = 168.
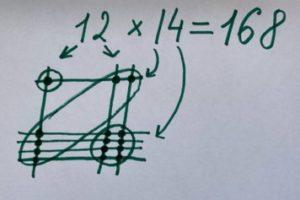
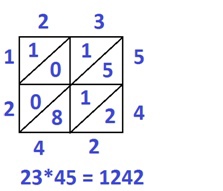
Метод решетки
Это очень простой метод, пришедший к нам от древних индусов. Покажем в действии, как им нужно пользоваться.
Нам нужно узнать, сколько будет 23х54:
1. Записываем число 23 горизонтально, а 54 – вертикально
2. Чертим между ними таблицу (решетку) 2х2 клетки – по количеству цифр в множителях. Каждую клетку делим пополам диагональной чертой от верхнего правого угла клетки – к нижнему левому.
3. Перемножаем каждую цифру первого числа с каждой цифрой второго и записываем результаты произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого ответа получим сложением цифр в косых полосах, двигаясь по часовой стрелке, начиная с правой нижней клетки: 2, 5 + 1 + 8 и т.д. Запишем результаты под таблицей и слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы).
Получим результат: 1242